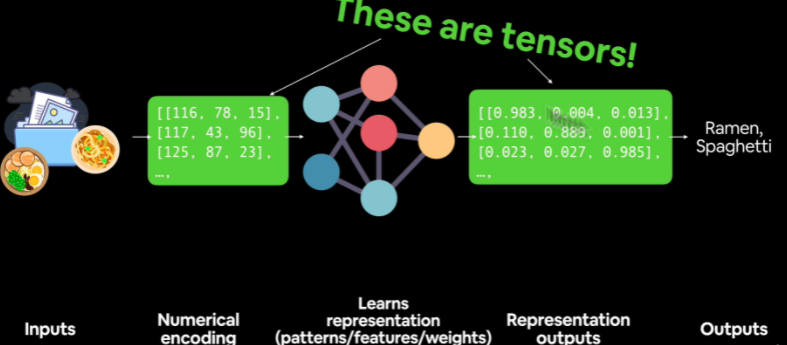
Each index of a tensor ranges over the number of dimensions of space. However, the dimension of the space is largely irrelevant in most tensor equations (with the notable exception of the contracted Kronecker delta).

1. Tensors are generalizations of scalars (that have no indices), vectors (that have exactly one index), and matrices (that have exactly two indices) to an arbitrary number of indices.
2. Tensors provide a natural and concise mathematical framework for formulating and solving problems in areas of physics such as elasticity, fluid mechanics, and general relativity.

Tensors, a crucial concept in the field of machine learning, deep learning, and data science, often become a stumbling block for many learners. To fully grasp the idea, we'll break it down, explore examples, and demystify various related aspects such as rank, dimension, components, indices, size, and shape.

What are Tensors?

In simple terms, tensors are a generalization of scalars, vectors, and matrices. They can be seen as multidimensional arrays of numbers, with each dimension known as a rank.

1. A scalar is a single number, a tensor of rank 0.
2. A vector is an array of numbers, a tensor of rank 1.
3. A matrix is a 2D array of numbers, a tensor of rank 2.
4. A 3D array, or a "cube" of numbers, is a tensor of rank 3.

The ranks continue to increase to define higher dimensional spaces.

Breaking Down the Definition of a Tensor

The formal definition of a tensor, "An nth-rank tensor in m-dimensional space is a mathematical object that has n indices and m^n components and obeys certain transformation rules," often overwhelms beginners. So, let's simplify it:

1. "nth-rank tensor": Rank refers to the number of dimensions or indices the tensor has. For example, a rank 1 tensor is a vector (which has one dimension), a rank 2 tensor is a matrix (which has two dimensions), and so on.
2. "m-dimensional space": This refers to the size of each dimension. For a matrix (rank 2 tensor), this would be the number of rows and columns.
3. "m^n components": Components are the individual elements or data points that make up the tensor. For example, in a matrix, each number is a component.

Simplifying with Examples

Consider a 3x3 image with three color channels (Red, Green, Blue). It is represented as a 3D array or a rank 3 tensor, with dimensions of 3 (height) x 3 (width) x 3 (color channels). It would have 3^3 or 27 components (individual color values for pixels).

Delving Deeper: Case of a 4x4 Image

Let's take a more specific example: a 4x4 pixel image with three color channels. Here, the tensor would have a rank of 3 (height, width, and color channels). The dimensions would be 4 (height) x 4 (width) x 3 (color channels), and there would be 4^3 or 64 components.

The indices here refer to the position of each component within the tensor. For example, you might reference the red color value of the pixel in the second row and third column as [2,3,1], where '2' refers to the row, '3' refers to the column, and '1' refers to the red channel.

The size of this tensor would be calculated by multiplying the sizes of all its dimensions together, resulting in 4 (height) x 4 (width) x 3 (color channels) = 48. The shape of this tensor would be (4, 4, 3), describing the number of elements along each dimension.

Difference Between Rank and Dimension

While both terms describe the structure of a tensor, they represent different aspects. The rank is the number of dimensions, while the dimensions refer to the size (or length) of each of those dimensions. In the case of our 4x4 pixel image tensor, the rank is 3, and the dimensions are 4, 4, and 3.

Sample Log of a 4x4x3 Tensor

A 4x4 pixel image with three color channels can be represented as a 3D array (or rank 3 tensor). Each pixel's color is represented by a 3-element vector (for the three color channels), and the image consists of a 4x4 grid of such pixels, giving us a shape of (4, 4, 3).

A 4x4 pixel image with 3 color channels could be represented as a 4x4x3 tensor, like this:

tensor = [
    [  # First row of pixels
        [230, 10, 10],    # Red-ish
        [230, 230, 10],  # Yellow-ish
        [10, 230, 10],   # Green-ish
        [10, 230, 230]   # Cyan-ish
    ],
    [  # Second row of pixels
        [10, 10, 230],   # Blue-ish
        [230, 10, 230],  # Magenta-ish
        [220, 220, 220], # Light gray
        [120, 120, 120]  # Gray
    ],
    [  # Third row of pixels
        [30, 30, 30],    # Dark gray
        [230, 50, 10],   # Different shade of red
        [230, 230, 60],  # Different shade of yellow
        [10, 60, 230]    # Different shade of blue
    ],
    [  # Fourth row of pixels
        [40, 230, 40],   # Different shade of green
        [50, 10, 230],   # Another shade of blue
        [230, 40, 230],  # Another shade of magenta
        [10, 40, 10]     # Dark green
    ]
]

Clearing the Confusion Around "Dimension"

The term "dimension" can lead to some confusion. In the context of tensors, "dimension" often refers to the depth of nested lists, not the geometric or mathematical space that a vector might represent. So, a vector like [3, 4] is a rank-1 tensor (or one-dimensional array) because it involves no nesting of lists. Its shape is considered to be (2,) because it contains two elements.

In summary, tensors, while initially appearing complex, can be demystified and understood through the step-by-step breakdown of their components and properties. As multidimensional arrays, they provide the foundation for manipulating data in machine learning and deep learning, making them a fundamental concept for anyone delving into these fields.

Understanding Covariance & Contravariance

A vector can be expressed in terms of its contravariant or covariant components

CASE 1: Expressing in terms of contravariant components → vector described in terms of components with basis vectors

If we decrease the length of the “basic vectors” (in a vector space), then the number of components required to make up a vector increases. Because the index & the number of components change contrary to each other, they are known as contravariant components of a vector Describing a vector in terms of these contravariant components (eg : 2 i + 3 j + 4 k) is how we usually describe a vectors

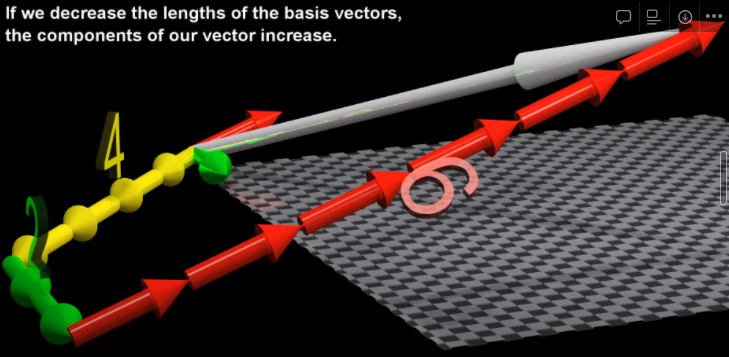
CASE 2: Expressing in terms of covariant components → vector described in terms of dot-product with basis vectorsIf we decrease the length of the basis vectors, then the dot-product decreases & vice versa. Since these properties are varying in the same way, we say that these are covariant components of a vector.

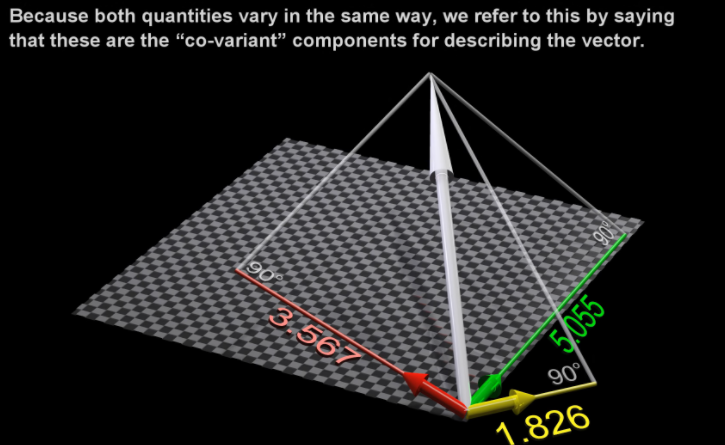
Specifying the notation for covariant & contravariant components

Now, say we take 2 vectors V & P

CASE 1: We multiply the contravariant values of V & P. On considering all possible ways, we get a matrix:

$$ \begin{bmatrix}   V^{1} P^{1} & V^{1} P^{2} &   V^{1} P^{3} \\ V^{2} P^{1} & V^{2} P^{2} &   V^{2} P^{3} \\ V^{3} P^{1} & V^{3} P^{2} &   V^{3} P^{3}    \end{bmatrix} $$

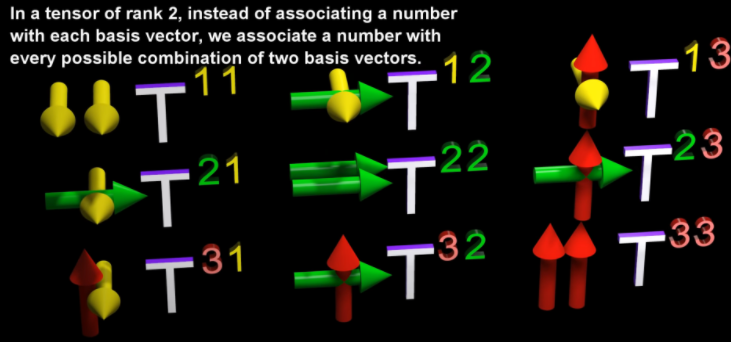
This will give us a tensor of rank 2 with 2 contra-variant index values. Here, each T value is called an element of this tensor. And since for each element, 2 indices (2 directional indicators are required) eg: Understanding by example, say we have a combination of 3 area vectors & 3 force vectors. To get the combination of all the forces on all the area vectors, for each such combination, we require 2 indices (i.e. 2 directional indicators → 1 for the force & 1 for the area). We get 9 components, each with 2 indices (referring to 2 basis vectors)

$$ \begin{bmatrix}   T^{11} & T^{12} &   T^{13}\\ T^{21} & T^{22} &   T^{23}\\ T^{31} & T^{32} &   T^{33}\end{bmatrix} $$

CASE 2: We multiply the covariant components of P with contravariant values of V . On considering all possible ways, we get a matrix:

$$ \begin{bmatrix}   V_{1} P^{1} & V_{1} P^{2} &   V_{1} P^{3} \\ V_{2} P^{1} & V_{2} P^{2} &   V_{2} P^{3} \\ V_{3} P^{1} & V_{3} P^{2} &   V_{3} P^{3}    \end{bmatrix} $$

This will give us a tensor of rank 1 co-variant index value & 1 contra-variant index value

$$ \begin{bmatrix}   T_{1}^{1} & T_{1}^{2} &   T_{1}^{3}\\ T_{2}^{1} & T_{2}^{2} &   T_{2}^{3}\\ T_{3}^{1} & T_{3}^{2} &   T_{3}^{3}\end{bmatrix} $$

CASE 3: We multiply the covariant values of V & P. On considering all possible ways, we get a matrix:

$$ \begin{bmatrix}   V_{1} P_{1} & V_{1} P_{2} &   V_{1} P_{3} \\ V_{2} P_{1} & V_{2} P_{2} &   V_{2} P_{3} \\ V_{3} P_{1} & V_{3} P_{2} &   V_{3} P_{3}    \end{bmatrix} $$

This will give us a tensor of rank 2 with 2 contra-variant index values

$$ \begin{bmatrix}   T_{11} & T_{12} &   T_{13}\\ T_{21} & T_{22} &   T_{23}\\ T_{31} & T_{32} &   T_{33}\end{bmatrix} $$

What makes a tensor a tensor, is that, when the basis vectors change, the components of the tensor would change in the same manner as they would in one of these objects → thus keeping the overall combination the same

What is it about the combination of components & basis vectors that makes tensors so powerful → all observers in all reference frames agree, not on the components or the basis vectors → but on their combinations, because they are the same

Index & Rank of tensors

A tensor does not necessarily have to be created from vector components as is shown in these examples

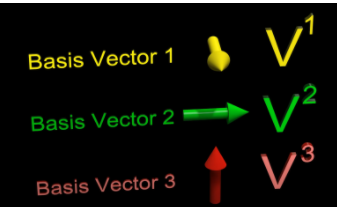
A tensor of rank 1 is a “vector” and has a number associated with each of the basis vectors. Only 1 index i.e. 1 combo of basis vectors is required to know the location

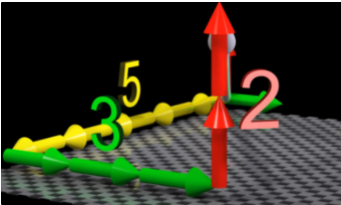
Here, \($V^1 = 5, V^2 = 3, V^3 = 2$\)

A tensor of rank 2 - we associate a number with every possible combination of 2 basis vectors

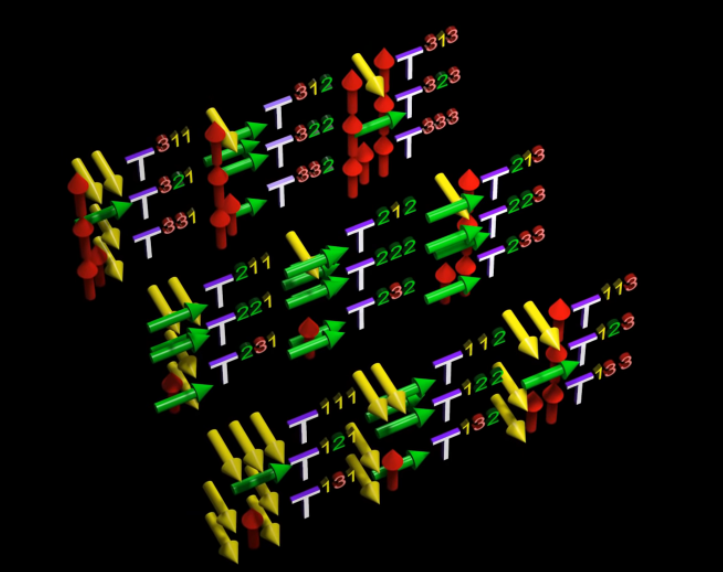
In a tensor of rank 3 - we associate a number with every possible combination of 3 basis vectors - composed of the components of 3 basis vectors. We can create different descriptions of this tensor by using different contravariant & covariant components of the basis vectors

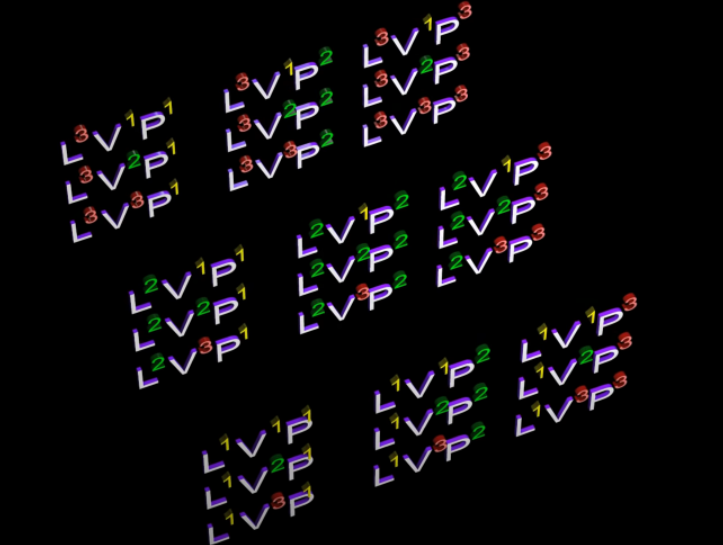
More mathematical facts

1. While the distinction between covariant and contravariant indices must be made for general tensors, the two are equivalent for tensors in three-dimensional Euclidean space (Euclidean space is the fundamental space of geometry, intended to represent physical space) , and such tensors are known as Cartesian tensors.
2. Objects that transform like zeroth-rank tensors are called scalars, those that transform like first-rank tensors are called vectors, and those that transform like second-rank tensors are called matrices. In tensor notation, a vector v would be written $v_i$, where i=1, ..., m, and matrix is a tensor of type (1,1), which would be written $a_i^j$ in tensor notation.
3. Tensors may be operated on by other tensors (such as metric tensors, the permutation tensor, or the Kronecker delta) or by tensor operators (such as the covariant derivative). The manipulation of tensor indices to produce identities or to simplify expressions is known as index gymnastics, which includes index lowering and index raising as special cases. These can be achieved through multiplication by a so-called metric tensor $g_{ij}, g^{ij}, g_i^j$, etc., e.g.,
4. Tensor notation can provide a very concise way of writing vector and more general identities. For example, in tensor notation, the dot product u·v is simply written u·v = $u_iv^i$ If two tensors A and B have the same rank and the same covariant and contravariant indices, then they can be added in the obvious way.
5. The generalization of the dot product applied to tensors is called tensor contraction, and consists of setting two unlike indices equal to each other and then summing using the Einstein summation convention. Various types of derivatives can be taken of tensors, the most common being the comma derivative and covariant derivative.
6. If the components of any tensor of any tensor rank vanish in one particular coordinate system, they vanish in all coordinate systems. A transformation of the variables of a tensor changes the tensor into another whose components are linear homogeneous functions of the components of the original tensor.

Tensors in the context of machine learning

The property of tensors to maintains its meaning under transformations is used also by machine learning, where real world data is transformed into corresponding tensors & then heavy calculations are done on these tensors to get valuable insights.

Reference videos

1. What is a tensor? - Link
2. Covariant & Contravariant Matrices - Link